Optimization for (simulation) engineering

“Efficient Global Optimization of Expensive Black-Box Functions” Jones, Schonlau, Welch, Journal of Global Optimization, December 1998

---

Engineering objective: optimize $f$ function/simulator, with lowest $f$ evaluations as possible.

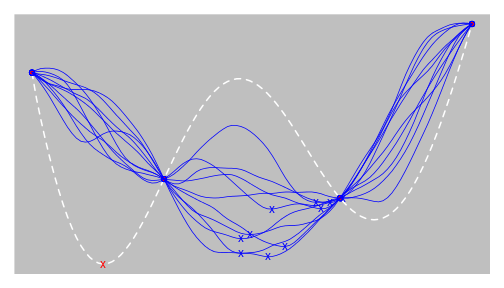
Basic idea

create some $\color{blue}{models\ of\ f}$ based on few evaluations $x={X}$

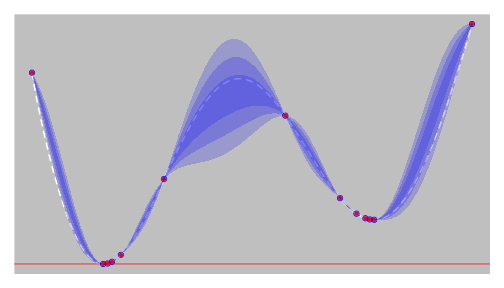
(simple) Kriging

$$\color{blue}M(x) = \mathcal{N}(m(x),s^2(x))$$

• $m(x) = C(x)^T C(X)^{-1} f(X)$
• $s^2(x) = c(x) - C(x)^T C(X)^{-1} C(x)$
• $C$ is the covariance kernel $C(.) = C(X,.)$, $c(.) = C(x,.)$

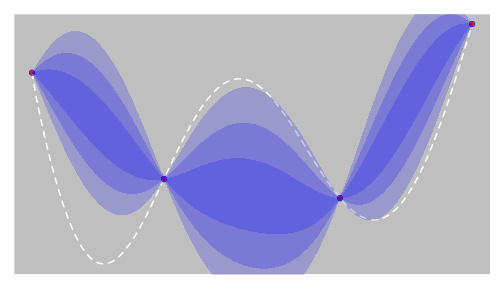
Efficient Global Optimization

</div>

Let’s define the Expected Improvement:

$$\color{violet}{EI}(x) = E[(min \{ f(X) \} - M(x))^+]$$

which is (also) analytical thanks to $M$ properties…

$$u(x) = { { min \{ f(X) \} - m(x) } \over { s(x) } }$$

$$\color{violet}{EI}(x) = s(x)\ \big(\ u(x)p_{\mathcal{N}}(u(x)) + d_{\mathcal{N}}(u(x))\ \big)$$

---

EGO: Maximize $EI(x)$ (*), compute $f$ there, add to $X$, … Repeat until …

---

• + good trade-off between exploration and exploitation
• + requires few evaluations of $f$
• - often lead to add close points to each others …
  Which is not very comfortable for kriging numerical stability
• - “one step lookahead” (myopic) strategy
• - rely on model suitability to $f$

(*) using standard optimization algorithm: BFGS, PSO, DiRect, …

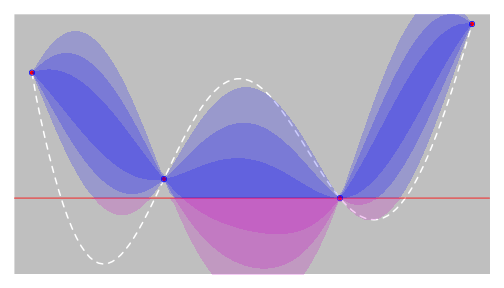
EGO - step 0

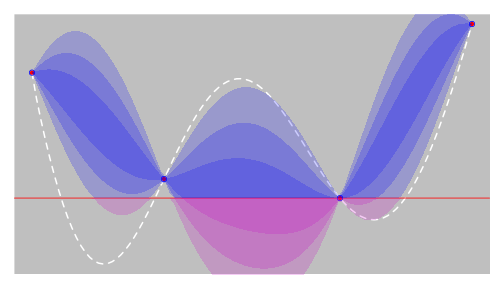
EGO - step 1

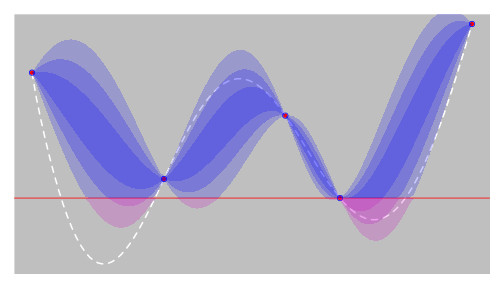
EGO - step 2

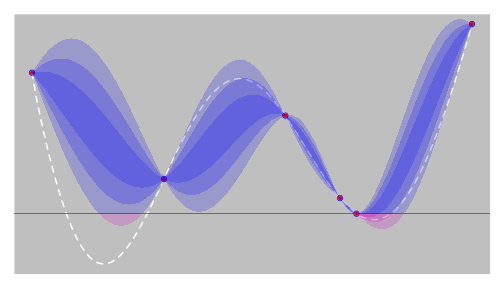
EGO - step 3

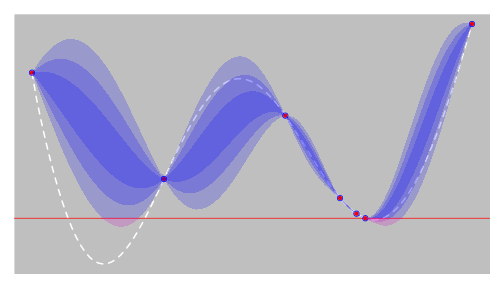
EGO - step 4

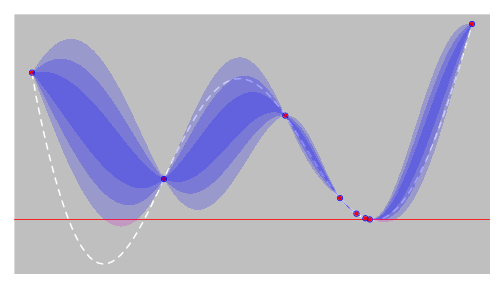
EGO - step 5

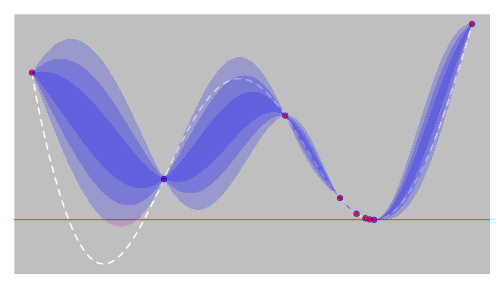
EGO - step 6

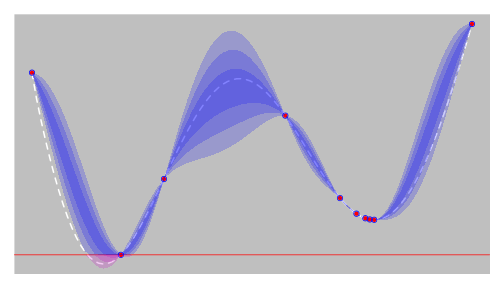
EGO - step 7

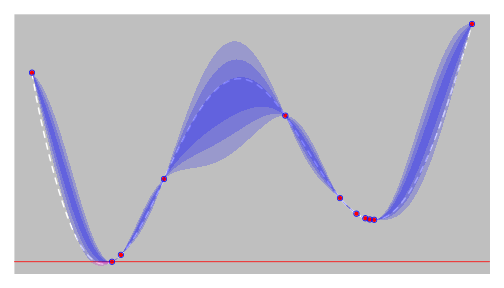
EGO - step 8

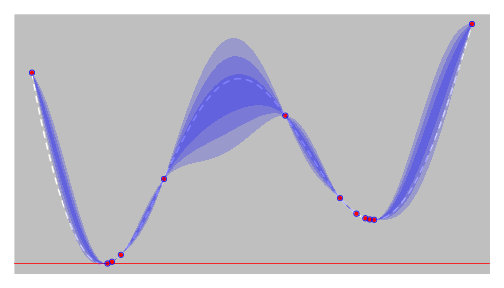
EGO - step 9